Let’s look at an example.

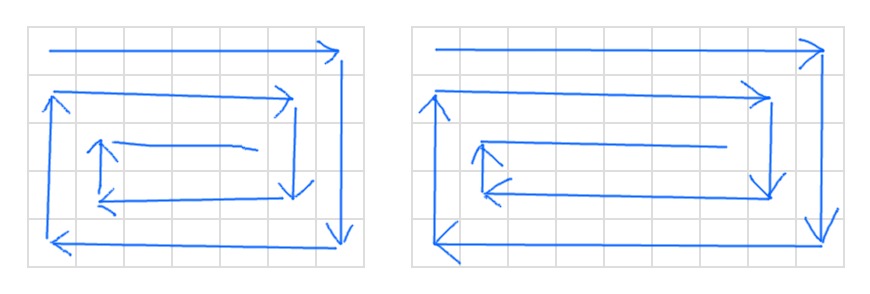
The two rinks require the same number of turns. What they have in common is the same number of rows, and the fact that the number of columns exceeds the number of rows. The number of turns is dependent on the magnitude of the greater dimension.

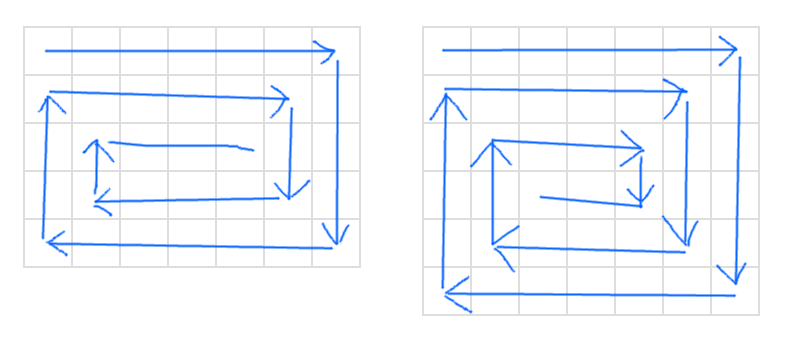
The second rink has one more row, and as a result, it has 2 more turns. Now, some edge cases.

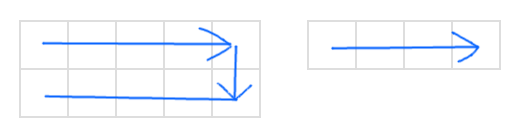
Let $X$ be the magnitude of the smallest row or column. We can formulate $2 \times (X - 1)$ as the number of turns. This expression also passes the two edge cases. Sub the actual value of $X$ to get the final formula $2 \times (\min(H, W) - 1)$.

Time complexity

$\mathcal{O}(1)$

Problem

Read the problem.