Mathematically find the last number. Since you are given the absolute distance from your guess to the answer, it is either above or below (positive or negative) the answer.

Let’s imagine the numbers on a number line. $A$ is the answer, $N_1$ and $N_2$ are the guesses, and $M_1$ and $M_2$ are the respective distances from the answer.

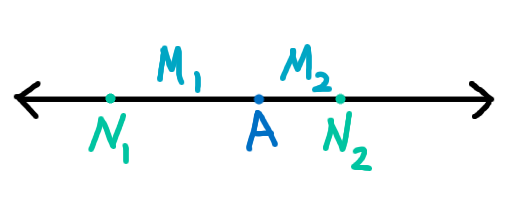
We can derive the equation $M = A − N$. For which in the example above, $M_1$ is positive and $M_2$ is negative. There are four cases of combinations of positive and negative differences ($M$), but we don’t need to check them all. We just need to know if $N_1 + M_1 = A$.

Let us use some equations. If $M_1$ is positive, then $N_1 + M_1 = A$, otherwise, it wouldn’t. We can use a system of equations to check if $M_1$ is positive. $\vert M_2\vert = A - N_2$. We are given differences as absolute values, so the equation is equivalent to $M_2 == A - N_2$. Then we plug in $A$: $M_2 = \vert N_1 + M_1 - N_2\vert$. If the equation holds true, then $M_1$ is positive (output $N_1 + M_1$), otherwise, $M_1$ is negative (output $N_1 - M_1$).

Time complexity

$\mathcal{O}(1)$

Problem

Read the problem.