Introduction

Greedy algorithms only take what they believe is the best path to the optimal solution and do not explore any other options, making them very efficient and usually simple. However, some problems are unsolvable with greedy algorithms because they require all options to be explored in order to find the optimal answer, in which case other techniques (e.g. dynamic programming) may be needed.

Example

To illustrate the concept of a greedy algorithm, the following problem is given:

Given an array with $N$ elements, choose $K$ elements such that the sum of the chosen elements is maximized.

One solution would be to generate all combinations of $K$ elements, and take the one with the largest sum. This method will have a complexity of $\mathcal{O}\binom{N}{K}$, or $\mathcal{O}\left(\frac{N!}{K!(N-K)!}\right)$, which is extremely slow for large arrays.

However, instead of exploring all the possible combinations of array elements, it is possible to solve this problem using a greedy solution: sorting the array and choosing the $K$ largest elements in the array.

This will always work because in order to maximize the sum of elements, the largest elements in the array must be chosen. Since only $K$ elements can be chosen, it is always optimal to greedily take the $K$ largest elements in order to maximize the sum.

Shown below is a code snippet of the greedy solution to the problem given:

Arrays.sort (arr); // Sorts array in ascending order
int sum = 0;

for (int k = N - 1; k >= N - K; k--) { // Iterates through and sums K largest elements
	sum += arr [k];
}
return sum;

Time complexity

$\mathcal{O}(N\log N)$, due to the sorting of the array.

Limitations

There are many problems which cannot be solved for all cases with a greedy algorithm. One example is given here:

Given $N$ types of coins, each worth a unique amount, find the minimum number of coins needed to make exactly $S$ dollars?

A greedy algorithm for this problem might go like this: start with the coin that is worth the most, use as many as possible, and move on to the next lowest coin value and do the same. This keeps going until all $S$ dollars are made.

Shown below is the implementation of this greedy algorithm:

Arrays.sort(coins); // Sorts coin array in ascending order by value
int used = 0;

for (int n = N - 1; n >= 0; n--) { // Iterates through coins in descending order by value
	while (coins[n] <= S) { // Keep using a certain coin to make change as long as it is possible to do so
		S -= coins[n];
		used++;
	}
}

return used;

If we are given the coin values of $$1$, $$5$, $$10$, $$25$, and $$50$, what is the smallest number of coins that are needed to represent $$41$? When using the greedy algorithm, we can start with one $$25$ coin. Now we have to make change for $$16$. We can use a $$10$ coin, a $$5$ coin and finally a $$1$ coin — four coins in total.

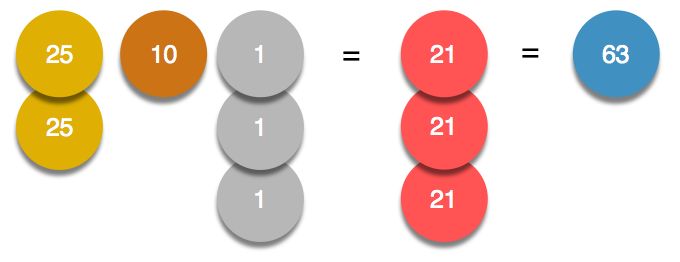
In the above case, the greedy algorithm worked perfectly. However, if we are given the coin values of $$1$, $$5$, $$10$, $$21$, $$25$ and are asked to make change for $$63$, the greedy algorithm would fail. It would suggest to use two $$25$ coins, one $$10$ coin, and three $$1$ coins for a total of six coins. However, the optimal solution would be to use three $$21$ coins.

Conclusion

Greedy algorithms are powerful tools that can be used to solve many problems quickly and efficiently. However, greedy algorithms commit to potentially suboptimal decisions early (which is often irreversible), and not all problems can be solved in a greedy manner as a result. Care must be taken to ensure that the greedy algorithm will never overlook the optimal solution in favour of short term gain.

Practice

MWC ‘15 Contest 1 P1: Playlist Panic
CCC ‘15 S2: Jerseys
CCC ‘16 S2: Tandem Bicycle
DMOPC ‘14 Contest 2 P3: Sawmill