Introduction

Sieve is a very fast algorithm for generating prime numbers within a range. You can tell whether or not a number is prime in constant time (great for answering queries). However, the algorithm requires the use of a large array.

The algorithm is based on the fact that a multiple of a prime number, other than itself, cannot be a prime number.

First, a boolean array is created in the size up to the maximum number (we will call this number $M$) initialized to true, except for 0 and 1. The array holds whether or not the number has been discovered as a prime number.

Loop through all the numbers in the range $[2, \sqrt{M}]$, we will see why. If the current number is a prime, then loop through its multiples (we will call the current number $n$) and set their prime status to false. However, as an optimization, some of the multiples would have already been set to false, so we need not to start from $2n$. All the primes below $n^2$ would have already been found and their multiples processed. Thus, we can start the next loop from $n^2$. Similarly, we only need to loop through the numbers in the range $[2, \sqrt{M}]$ because after $\sqrt{M}$, any prime numbers found would only disprove the primeness of numbers that are past the range.

Depending on what we want to do, we can loop through the prime array again and generate a list of all the prime numbers. Or maybe we want to check whether or not a number is prime.

Visualization

Visualization of the algorithm on the range $[1, 100]$. Gold indicates a prime number. The flashing row at the end shows that the search is done – all the numbers up to $\sqrt{100}=10$ have been checked.

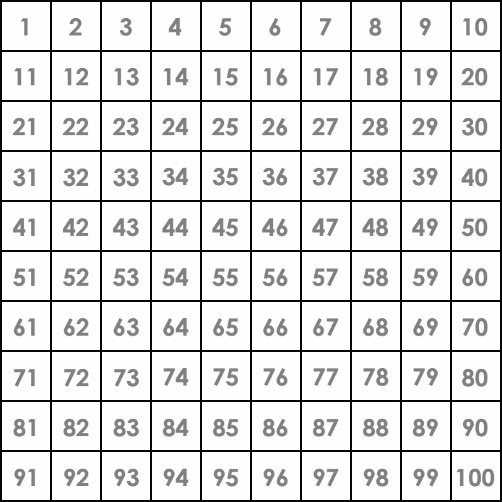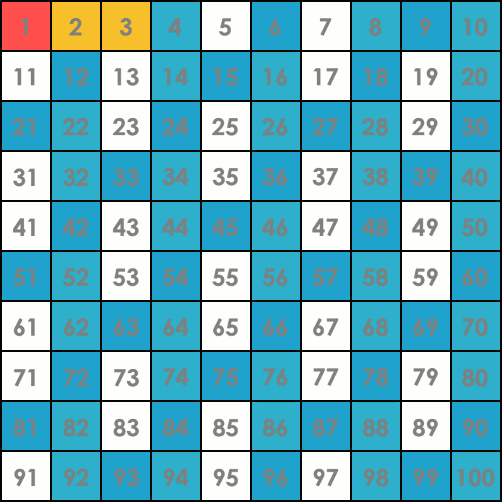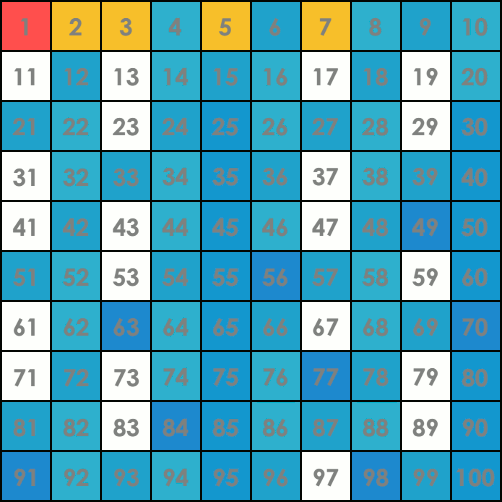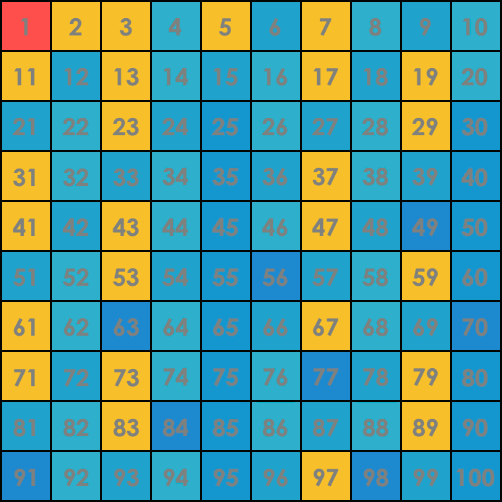
Implementation

boolean[] isPrime = new boolean[M + 1];
Arrays.fill(isPrime, true); // Need to import java.util.Arrays;
isPrime[0] = false;
isPrime[1] = false;

for (int i = 2; i * i <= M; i++) {
	if (isPrime[i]) {
		for (int j = i * i; j <= M; j += i)
			isPrime[j] = false;
	}
}

// Optional: Generate a list of primes
ArrayList<Integer> primes = new ArrayList<Integer>();
for(int i = 2; i <= M; i++)
	if(isPrime[i]) primes.add(i);

Time complexity

$\mathcal{O}(M \log \log M)$, where $M$ is the maximum to calculate to.

Space complexity

$\mathcal{O}(M)$, where $M$ is the maximum to calculate to.

Practice

MWC ‘15 #6 P2: Breadwinners
DMOPC ‘15 Contest 1 P4 - Itami and Candy
DMOJ: The Third Cellar
FHC ‘15 Round 1: Homework (requires modifying the algorithm)