Introduction

The following is a diagram of a queue. It is depicted as a linear structure. The first element is called the front. It is the next element to be removed. Conversely, the last element is called the back. It is the most recently inserted element.

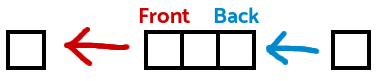
Elements may only be inserted to the back and removed from the front.

Example

To understand how a queue might be used to solve programming problems, let’s solve a simple problem:

There are $N$ customers waiting in line, each wanting to buy a certain amount of bread slices. $Q$ events occur, where each one is one of two types:

Type 1: A customer goes to the back of the line, with a certain amount of bread slices.

Type 2: The customer at the front of the link leaves the line without purchasing any bread.

Everyone remaining buys the bread they have. Output how many slices of bread are sold.

To solve this problem, use a queue to represent the customers waiting in line, as shown below:

import java.util.*; // Import the required classes.

// Create a queue which stores integers, representing the amount of bread slices each customer wants to buy.
Deque<Integer> queue = new ArrayDeque<Integer>();

When an event of type 1 occurs, we add the customer to the back of the line, as shown below:

queue.addLast(s); // Add a customer who wants s slices of bread to the back of the line.

When an event of type 2 occurs, we remove the customer at the front of the line, as shown below:

queue.removeFirst(); // Remove the customer at the front of the line.

Finally, after all $Q$ events are over, we can simply sum up all the bread slices held by customers remaining in the line, as shown below:

int total = 0;

while (!queue.isEmpty()) { // As long as there are still people in the queue.
	total += queue.removeFirst(); // Remove them from the line and add their bread slices to the total.
}

return total;

Conclusion

Queues are extremely important data structures that are used in many programming problems, especially in the field of graph theory, where they are most commonly associated with BFS algorithms. While they are rarely the only part of a solution to a problem, they are used as utility data structures in many solutions.