Introduction

The following is a diagram of a stack. It is depicted as a linear structure. The last element inserted is called the top.

Elements may only be inserted into and removed from the top.

Example

To understand how a stack might be used to solve programming problems, let’s solve a simple problem:

Given a string consisting only of ( and ) characters, check if all parentheses are nested properly.

Example of correctly nested parentheses include: (()), ()()(), and ()(()()).

Example of incorrectly nested parentheses include: ()), ()(((), and )(()()).

To solve this problem, realize that as you read the expression from left to right, the most recent open bracket always matches the first close bracket, as shown in the diagram below:

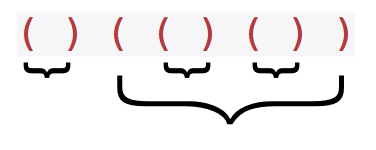
Using this information, we can form an algorithm. We will iterate through the expression left to right. If a ( character is encountered, it will be added to the stack. If a ) character is encountered, we will remove a ( character from the stack, as it has been matched. If there is no ( to remove from the stack, it means that the expression is unbalanced. The expression is also unbalanced if the stack still has elements after the iteration is complete.

The following idea is expressed in the code snippet below. The snippet returns true if the expression is balanced and false if it is unbalanced.

import java.util.*; // Import the required classes.

boolean solve(String expression) {
// Create a stack which stores objects of type Character.
	Deque<Character> stack = new ArrayDeque<Character>();

	for (int n = 0; n < expression.length (); n++) {
		// If the character is an opening bracket, add it to the stack
		if (expression.charAt(n) == '(') {
			stack.addFirst('(');
		} else if(!stack.isEmpty()) { // If the character is a closing bracket and there is an opening bracket that came before it.
			stack.removeFirst();
		} else { // If the character is a closing bracket and there are no opening brackets that came before it, the expression is unbalanced.
			return false;
		}
	}

	// Expression is only balanced if there are no more opening brackets to be matched.
	return stack.isEmpty();
}

The above code is a simpler version of algorithms that solve BEDMAS equations. Those algorithms also use a stack to handle order of operations and ensure that the correct answer is found.

Recursion

The behaviour of recursion closely models how stacks add and remove elements. For example, shown below is a method which recursively calculates the factorial of a given number:

public static int factorial(int n) {
	if (n <= 1) {
		return 1;
	}

	return n * factorial(n - 1);
}

Imagine a stack which holds a list of methods to execute, where the methods at the top of the stack are to be executed first. If factorial(3) is called, it will be added to the stack.

Inside factorial(3), the method factorial(2) is called. Since the result of factorial(3) depends on factorial(2), factorial(2) must be executed first, thus it will be placed on top of the stack.

factorial(2) will then call the method factorial(1), which is placed on top of the stack. Since factorial(1) doesn’t make any recursive calls, it will return a result of 1, and is removed from the top of the stack.

factorial(2) is now on top of the stack and since it doesn’t make anymore recursive calls, it returns a value of 2 and is removed from the stack.

Now, just factorial(3) is left on the stack. Finally, factorial(3) is removed from the stack, and a final answer of 6 is returned.

Because recursive calls can be easily modelled with stacks, any recursive method can be rewritten to avoid recursion, and use a stack instead. Shown below is the above factorial() method rewritten to use a stack:

public static int factorial(int n) {
	Deque<Integer> stack = new ArrayDeque<Integer>();
	stack.addFirst(n);

	int result = 1, curr = 0;

	while (!stack.isEmpty()) {
		curr = stack.removeFirst();
		result *= curr;

		if (curr > 1) {
		  stack.addFirst(curr - 1);
		}
	}

	return result;
}

Rewriting a recursive method to use a stack can sometimes avoid stack overflow errors, which can occur for methods which make a large amount of recursive calls.

Conclusion

Stacks are extremely important data structures that are used in many programming problems, especially in the field of graph theory, where they are most commonly associated with DFS based algorithms. While they are rarely the only part of a solution to a problem, they are used as utility data structures in many solutions.

Practice

CCC ‘15 S1 - Zero That Out
CCC ‘14 S3 - The Geneva Confection
MWC ‘15 #2 P2: Towering Towers